Half Integer

Xiu-Zhe (Roger) Luo's Blog

0%

Implement Your Own Automatic Differentiation with Julia in ONE day

Posted on Edited on Disqus:

I was playing with AutoGrad.jl and Zygote.jl, they both look
awesome, and AutoGrad.jl has already been applied to the machine learning framework in Julia: Knet.jl. When I tried to read the source code of AutoGrad.jl, it is actually quite simple and small.

But, as a PyTorch contributor and user, I personally prefer some of PyTorch’s interfaces (both frontend and backend), and as a Julian, I want to see how simple it can be to write a Julia AD package. Therefore, I tried to implemented my own automatic differentiation and it just took me one day to finished the core part (including broadcast!).

Although, I spent a few hours more during the next following days to polish the interface (a weekend to write a blog post). But it is actually quite easy to implement an automatic differentiation package in Julia.

I packed it to a package (YAAD.jl: Yet Another AD package for Julia) here: Roger-luo/YAAD.jl

In this post, I’ll introduce how did I implemented my own automatic differentiation, and maybe, you can build one of your own as well!

Automatic Differentiation: A Brief Intro

There are generally two kinds of automatic differentiation: forward mode differentiation and reverse mode differentiation. What we need in deep learning (as well as tensor networks in physics) is the reverse mode differentiation, because the model we are going to optimize usually contains quite a lot parameters. This is also called as back-propagation and requires something called comput-graph.

Comput-Graph

To illustrate this, I stole some nice picture and re-ploted them in animation from cs5740, 2017sp, Cornell.

Say we are calculating the following expression:

$$
y = \mathbf{x}^T \mathbf{A} \mathbf{x} + \mathbf{b}\cdot \mathbf{x} + c
$$

We will need to call several functions in Julia to get the result $y$, which is

  1. $\mathbf{z_1} = \mathbf{x}^T$: transpose function.
  2. $\mathbf{z_2} = \mathbf{z_1} A$ matrix-vector multiplication, which can be gemv in LinearAlgebra.BLAS, or just *.
  3. $y_1 = \mathbf{z_2} \mathbf{x}$ vector dot operation, which is LinearAlgebra.dot or the UTF-8 operator x ⋅ y
  4. $y_2 = \mathbf{b} \cdot \mathbf{x}$ another vector dot
  5. $y_1 + y_2 + c$ a scalar add function, one can calculate it by simply calling + operator in Julia.

In fact, we can draw a graph of this expression, which illustrates the relationship between each variable in this expression.
Each node in the graph with an output arrow represents a variable and each node with an input arrow represents a function/operator.

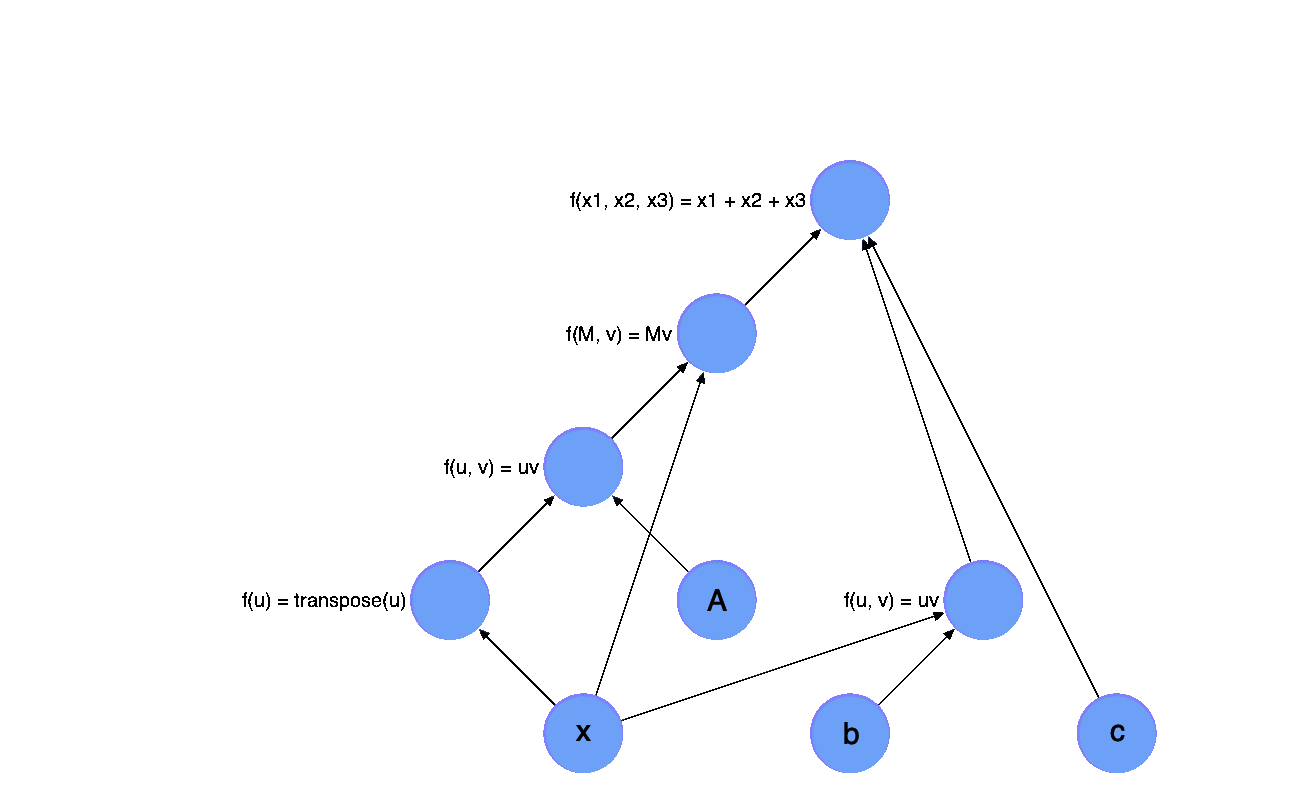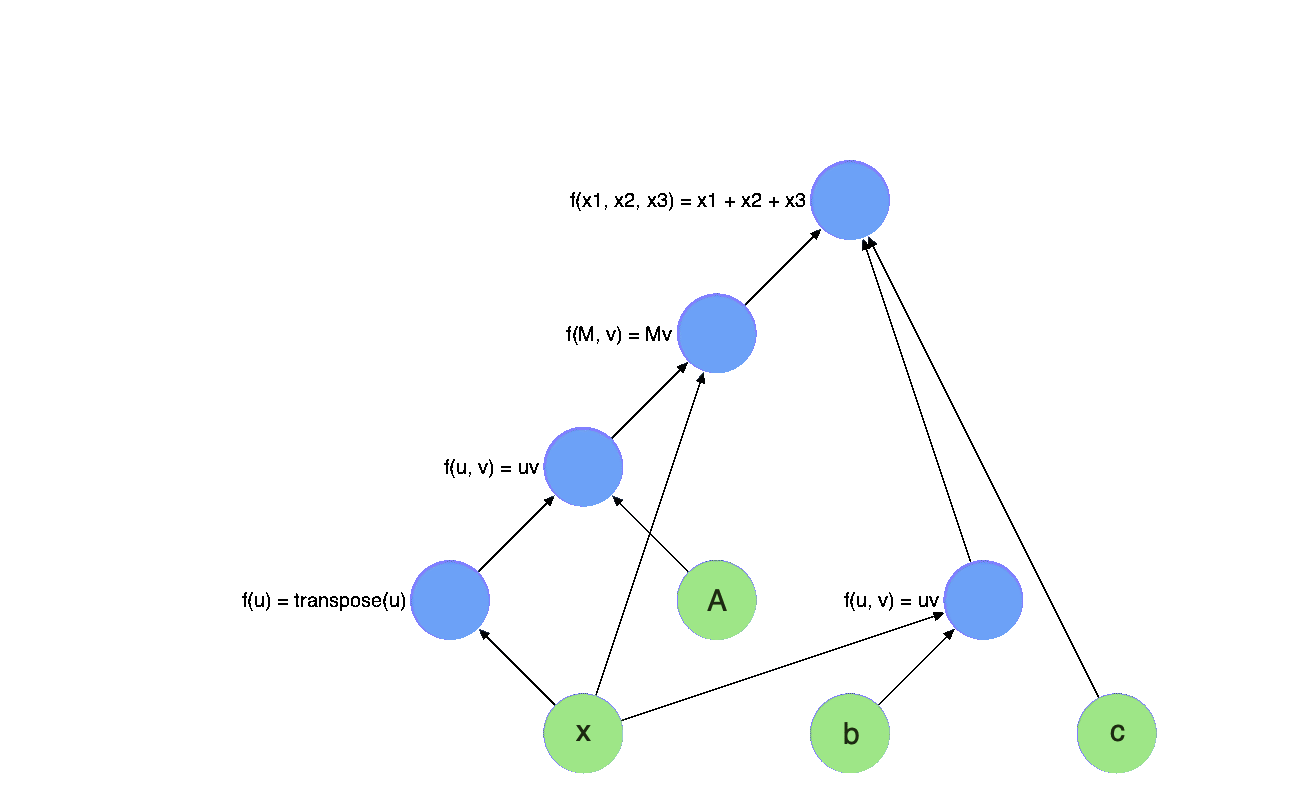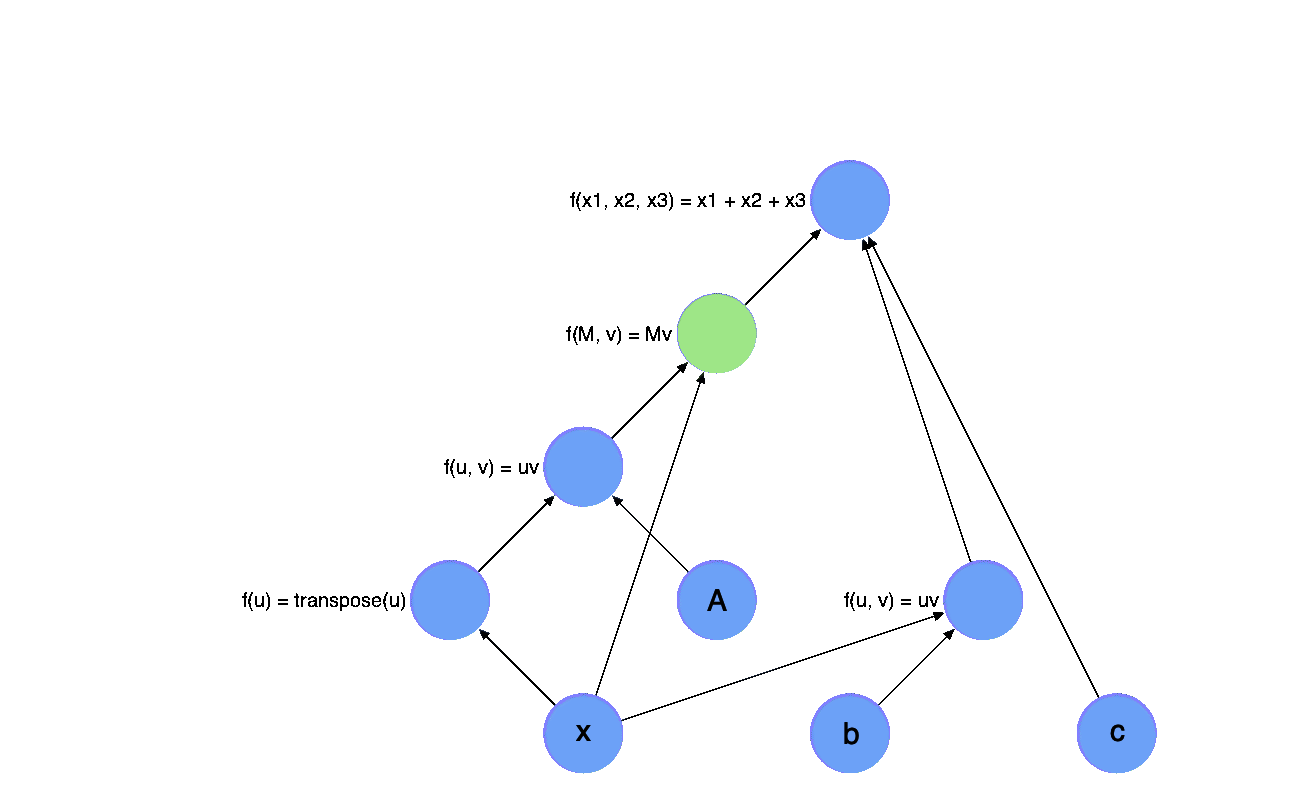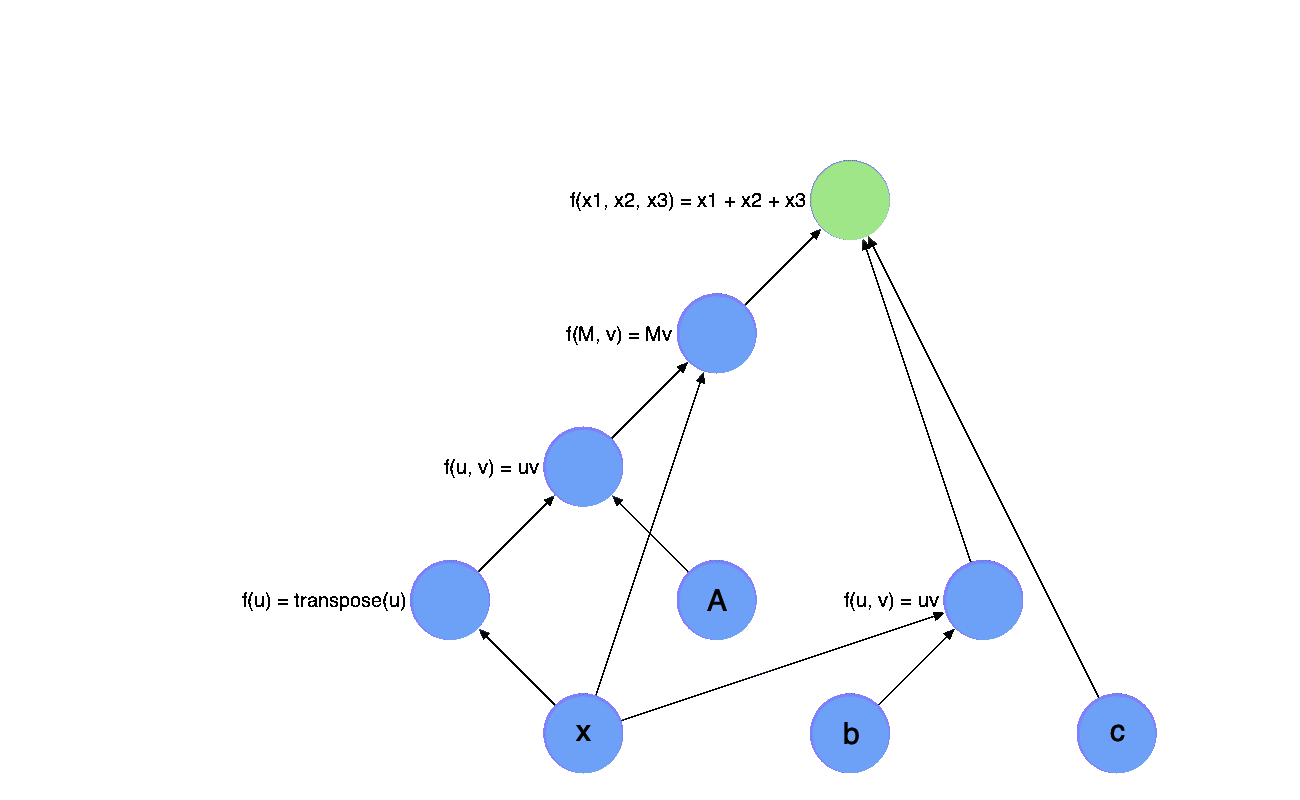
comput-graph

The evaluation of the math equation above can then be expressed as a process called forward evaluation, it starts from the leaf nodes, which represents the inputs of the whole expression, e.g they are $\mathbf{x}, \mathbf{A}, \mathbf{b}, c$ in our expression. Each time, we receive the value of a node in the graph, we mark the node with green.

Now, let’s calculate the gradients with chain rule, the number of gradients returned by each function is the same as their inputs. We mark the node red if we receive a gradient, the gradient will be back propagated through the graph, which is called back propagation or backward evaluation.

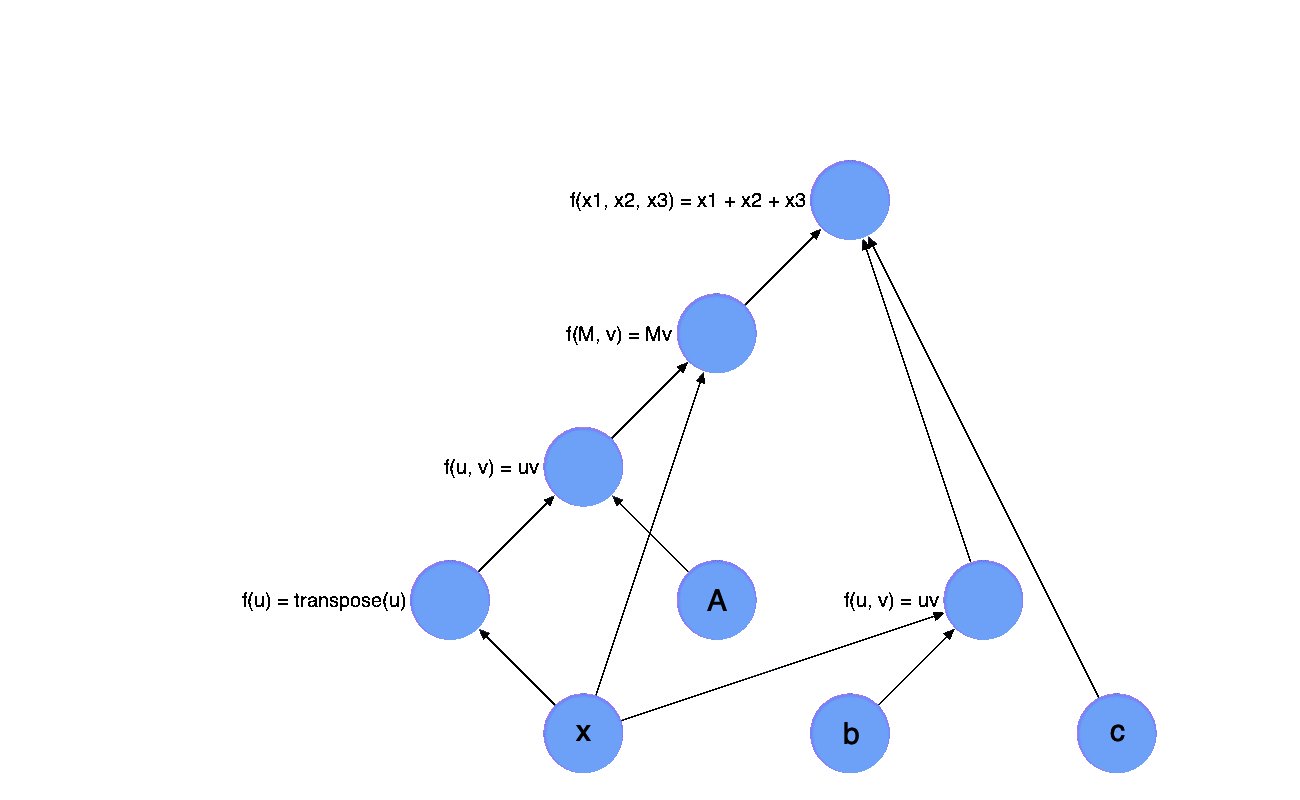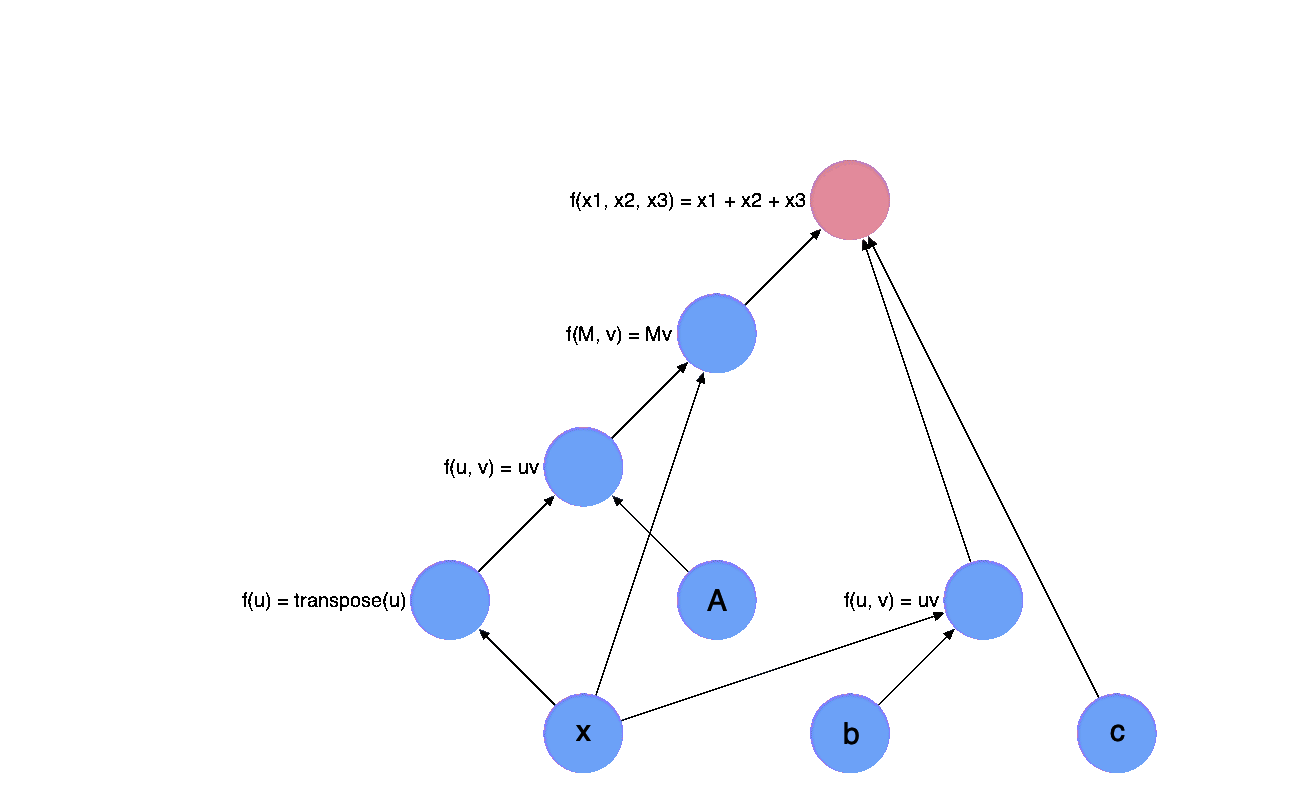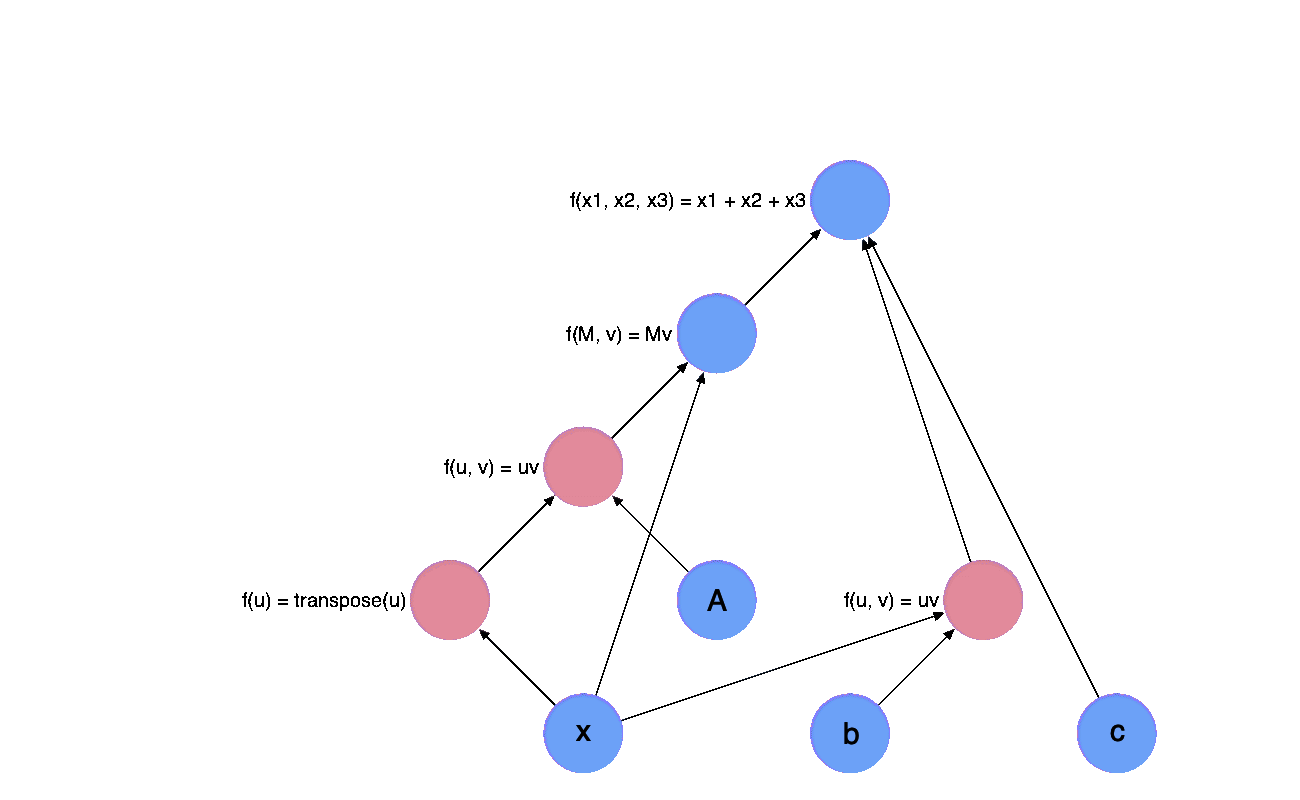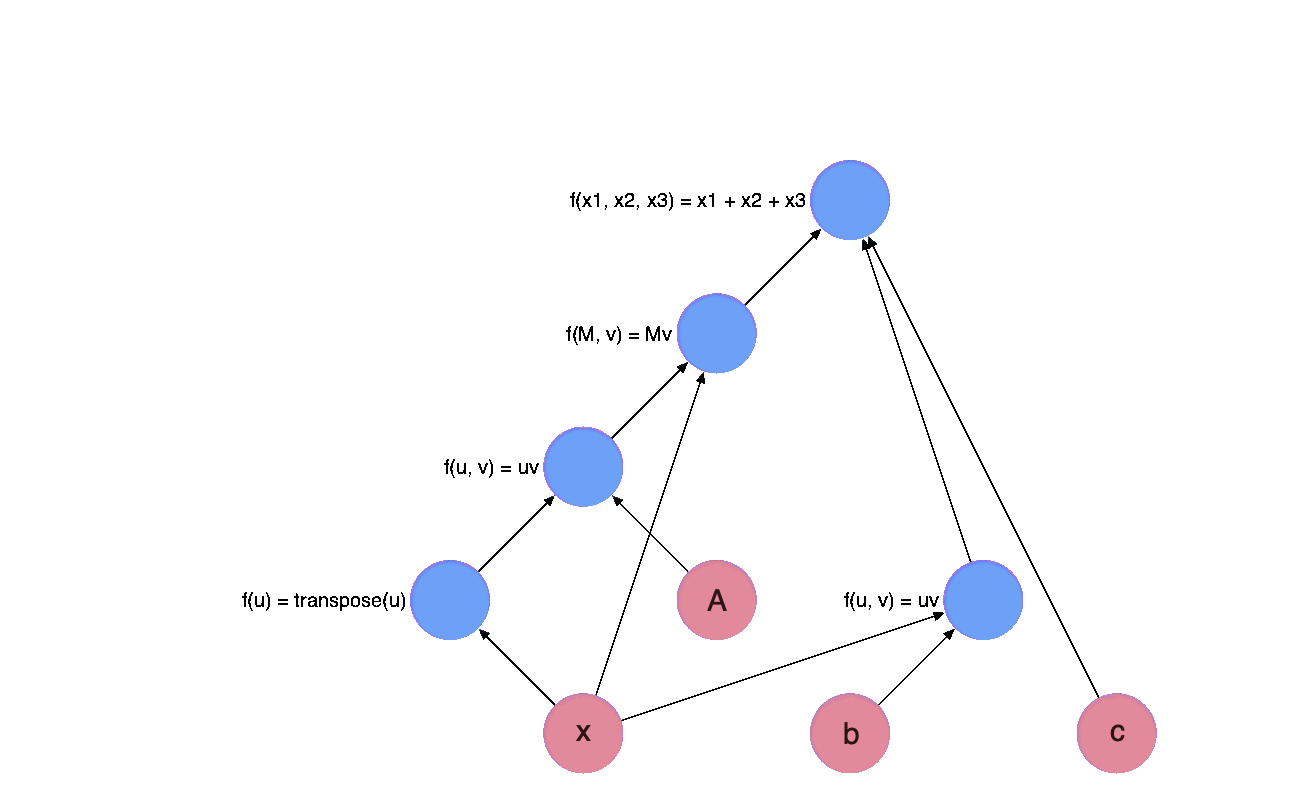
comput-graph

Dynamic Comput Graphs VS Static Comput Graphs

Although, the way of forward evaluation and backward evaluation are actually the same, but for implementation, we can construct the graph on the fly (like in PyTorch) or as a static declaration (like in TensorFlow).

Generally, the difference between them is that:

Whether the graph is defined before the forward evaluation happens or along with the forward evaluation.

I’m a PyTorch syntax lover, so I’m going to implement my AD as a dynamic constructed graph. But I’m also planning to write a macro in Julia that “freeze” a dynamic graph to static graph, because in principle, static graph is easier to optimize, since we will be able to access the whole graph before evaluation happens, which allows us to dispatch methods statically, but static graphs can be hard to debug.

Define the Nodes in the Computational Graph

Well, before we start writing something concrete, we can first define an abstract type for all nodes we are going to define:

1
abstract type AbstractNode end

Leaf Nodes

Same, define an abstract type first.

1
abstract type LeafNode <: AbstractNode end

In PyTorch, a Variable is a multi-dimensional array (tensor) with a gradient (also store in a multi-dimensional array of the same size and data type). And it will accumulate the gradient if we back-propagate the graph for multiple times.

Accumulating is sometimes useful, when you want to calculate the expectation of the gradient, or manipulate a batch of data, but not always useful. But anyway, we have an abstract type, we can define different flavored leaf nodes later.

1
2
3
4
5
6
7
mutable struct Variable{T} <: LeafNode
    value::T
    grad::T

    Variable(val::T) where T = new{T}(val)
    Variable(val::T, grad::T) where T = new{T}(val)
end

Here, we use incomplete initialization, since we don’t really need to allocate a memory for the gradient at the beginning, we can just take the ownership of a temporary variable’s memory later.

Other Nodes

Well, now we have some leaf nodes, but we need to store operations and their output for later use, so firstly, I define something called Node

1
2
3
4
5
struct Node{FT <: Function, ArgsT <: Tuple, KwargsT <: NamedTuple} <: AbstractNode
    f::FT
    args::ArgsT
    kwargs::KwargsT
end

It is a subtype of AbstractNode, and it stores a function call’s arguments and keywords. However, we will need to consider
broadcast and normal function calls, they are actually different, therefore we should not directly store the function, thus, so let’s write some traits:

1
2
3
4
5
6
7
8
9
10
11
12
13
abstract type Operator end

module Trait
import YAAD: Operator

struct Method{FT} <: Operator
    f::FT
end

struct Broadcasted{FT} <: Operator
    f::FT
end
end # Trait

Now we change Function to Operator

1
2
3
4
5
struct Node{FT <: Operator, ArgsT <: Tuple, KwargsT <: NamedTuple} <: AbstractNode
    f::FT
    args::ArgsT
    kwargs::KwargsT
end

And we may make some constructors for convenience, since most fs will be method calls rather than broadcasts or self-defined
operators, and we usually don’t need the keyword arguments either:

1
2
3
# wrap function to Method
Node(f::Function, args, kwargs) = Node(Trait.Method(f), args, kwargs)
Node(op, args) = Node(op, args, NamedTuple())

In fact, Node is actually just a trait for some object (some subtype of Operator), we haven’t
defined the type that store the output of each node in the graph, so here let’s define a CachedNode
which will cache the forward evaluation result of Node:

1
2
3
4
mutable struct CachedNode{NT <: AbstractNode, OutT} <: AbstractNode
    node::NT
    output::OutT
end

So, to store the forward evaluation result of a Node with CachedNode when it is constructed, we need to forward propagate
the comput-graph recorded in Node and assign it to the cache:

1
2
3
4
5
function CachedNode(f, args...; kwargs...)
    node = Node(f, args, kwargs.data) # this constructs a Node
    output = forward(node)
    CachedNode(node, output)
end

Evaluations

The evaluation is the most important part, because we want to define our rules of evaluation in an extensible way, and
try to make it efficient. Luckily, in Julia, we have multiple dispatch! Let’s make use of it!

Forward Evaluation

But how do we forward evaluate a Node? This depends on what kind of method is implemented for this generic function forward:

  1. If input is a Node, we re-dispatch this method to its operator’s forward method (while it forward evaluates the args and kwargs):
1
forward(node::Node) = forward(node.f, map(forward, node.args)...; map(forward, node.kwargs)...)

This will allow us to tweak the forward evaluation by simply implementing a method for the generic function forward, e.g, if we don’t want to directly calculate the result of a linear operator $\mathbf{W}\mathbf{x} + \mathbf{b}$ rather than store two nodes separately (a matrix-vector multiplication * and an add function +).

1
2
3
4
5
6
struct Linear <: Operator
  w::Matrix{Float64}
  b::Vector{Float64}
end

forward(op::Linear, x::Vector{Float64}) = op.w * x + b
  1. If input is a CachedNode, this means our user is evaluating this node for the second time (since we calculate the result when construct it), we will update its output
1
forward(node::CachedNode) = (node.output = forward(node.node))
  1. However, for simple function calls, we don’t want to write something like
1
2
3
function forward(::Method{typeof(sin)}, x)
  sin(x)
end

each time, let’s make it simpler, by re-dispatching an operator’s forward method to a function call:

1
forward(op::Operator, args...; kwargs...) = op.f(args...; kwargs...)

This means, as long as, the operator defines its own call method, it does not need to implement a method for forward, e.g

We can just define the call method for Linear rather than defining a method for forward:

1
(op::Linear)(x::Vector) = op.w * x + b
  1. There could be some constants in the Node, e.g when we call Variable(2.0) + 1.0, this 1.0 is actually a constant, therefore, we can just return it, when the input is not part of the computational graph (not a subtype of AbstractNode) and define a default method for AbstractNode for better error messages.
1
2
forward(x) = x
forward(x::NT) where {NT <: AbstractNode} = error("forward method is not implemented for node type: $NT")
  1. For leaf nodes, they should directly return their value, but we might use another kind of leaf node to make the non-PyTorch lover
    happy in the future, so let’s define a generic function value to get this property:
1
2
3
4
5
6
7
8
9
10
11
12
value(x) = x

function value(x::T) where {T <: AbstractNode}
    error(
        "Expected value in this node $x of type $T ",
        "check if you defined a non-cached node",
        " or overload value function for your node."
    )
end

value(x::Variable) = x.value
value(x::CachedNode) = value(x.output)

And leaf nodes’ forward directly return its value:

1
forward(node::LeafNode) = value(node)

Okay! We have defined all we need for forward evaluation, now let’s try to implement backward evaluation.

Backward Evaluation

The backward evaluation is actually similar to forward evaluation, we will call backward recursively on each node and its args (no, I’m not going to support backward on kwargs here, XD).

Firstly, for LeafNode, this is simple, e.g Variable will just take the grad

1
2
3
4
5
6
7
8
function backward(x::Variable, grad)
    if isdefined(x, :grad)
        x.grad += grad
    else
        x.grad = grad
    end
    nothing
end

We will check if this grad member is defined (it is incomplete initialized!), if it is not, we will just use the memory of
this gradient, or we can add it to the current gradient, just like PyTorch’s Variable (or Tensor after v0.4).

And now, we need to define how to backward evaluate a CachedNode:

  1. We gather the gradients of inputs from a function called gradient
  2. We put each corresponding gradient to sub-node of current node and call their backward
1
2
3
4
5
6
7
function backward(node::CachedNode, f, grad)
    grad_inputs = gradient(node, grad)
    for (each, each_grad) in zip(args(node), grad_inputs)
        backward(each, each_grad)
    end
    nothing
end

Oh, you might want to add some assertion to output a better error message here, we will check the type of gradient and output and also their size here, in most cases, gradient should have the exact same
type and size as output:

1
2
3
4
5
backward_type_assert(node::CachedNode{<:AbstractNode, T}, grad::T) where T = true
backward_type_assert(node::CachedNode{<:AbstractNode, T1}, grad::T2) where {T1, T2} =
    error("Gradient is expected to have the same",
          " type with outputs, expected $T1",
          " got $T2")

but for subtype of AbstractArray, we can just allow them to have the same static parameter (tensor rank and data type), because we will probably be dealing with SubArray and Array for some operators, which does not really matters

1
2
3
# exclude arrays
backward_type_assert(node::CachedNode{<:AbstractNode, T1}, grad::T2) where
    {T, N, T1 <: AbstractArray{T, N}, T2 <: AbstractArray{T, N}} = true

Finally we check the size of the gradients and outputs

1
2
3
4
5
6
7
function backward_size_assert(node::CachedNode, grad)
    size(node.output) == size(grad) ||
        error(
            "gradient should have the same size with output,",
            " expect size $(size(node.output)), got $(size(grad))"
        )
end

In Julia, there is a compiler option to turn bounds check off. We sometimes don’t actually need to check bounds at runtime
so we put this assertion in @boundscheck. It looks like:

1
2
3
4
5
6
7
8
9
10
11
function backward(node::CachedNode, f, grad)
    backward_type_assert(node, grad)
    # TODO: replace with @assert when there is a compiler option for it
    @boundscheck backward_size_assert(node, grad)

    grad_inputs = gradient(node, grad)
    for (each, each_grad) in zip(args(node), grad_inputs)
        backward(each, each_grad)
    end
    nothing
end

OK, now, let’s think about how to return the gradient, I would prefer our AD be highly extensible by taking advantage of Julia’s multiple dispatch, and I will only need to define the gradient by defining different methods for gradient, e.g

1
gradient(::typeof(sin), grad, output, x) = grad * cos(x)

This can be implemented in the same way as forward: re-dispatch the method to different syntax:

1
gradient(x::CachedNode, grad) = gradient(x.node.f, grad, x.output, map(value, x.node.args)...; map(value, x.node.kwargs)...)

Here we dispatch the gradient of a CachedNode directly to a method implemented for Operator, but we have the same situation with forward, we don’t want to write Method trait each time

1
2
gradient(x::Operator, grad, output, args...; kwargs...) =
    gradient(x.f, grad, output, args...; kwargs...)

Finally, define a default error massage:

1
2
3
4
5
6
7
8
9
gradient(fn, grad, output, args...; kwargs...) =
    error(
        "gradient of operator $fn is not defined\n",
        "Possible Fix:\n",
        "define one of the following:\n",
        "1. gradient(::typeof($fn), grad, output, args...; kwargs...)\n",
        "2. gradient(op::Trait.Method{typeof($fn)}, grad, output, args...; kwargs...)\n",
        "3. gradient(op::Trait.Broadcasted{typeof($fn)}, grad, output, args...; kwargs...)\n"
    )

So in this way, when we implement a specific method of some types for gradient, Julia will auto dispatch gradient to that method, e.g

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# I re-define the concrete type `Linear` here in order to store the gradient
struct Linear <: Operator
  w::Variable{Matrix{Float64}}
  b::Variable{Vector{Float64}}
end

function gradient(op::Linear, grad, output, x)
  grad_w, grad_b = # some gradient expression to calculate the gradient of w and b
  backward(op.w, grad_w) # update gradient of w
  backward(op.w, grad_b) # update gradient of b

  grad_input = # calculate the gradient of input
  grad_input # return the gradient of input
end

Umm, and finally, I would like to have an eye-candy function to construct a node (but this depends on you, it is not actually necessary):

1
register(f, args...; kwargs...) = CachedNode(f, args...; kwargs...)

Okay, let’s try to register an operator now!

1
2
Base.sin(x::AbstractNode) = register(Base.sin, x)
gradient(::typeof(Base.sin), grad, output, x) = (grad * cos(x), )

Remember we assumed gradient returns several gradients, the return of gradient has to be an iteratable of gradients.

Broadcast

However, for above gradients for scalars, this will just work. It won’t work for arrays. We will need to re-dispatch broadcast in Julia.

Let me introduce some basic concepts of the interface of broadcast in Julia first, and then we will find a very easy way
to implement AD for broadcast:

The whole broadcast mechanism is implemented in a module Broadcast in Base, each different type has its own BroadcastStyle (this is a trait). So what we need to do, is just to implement our own broadcast style and construct a
CachedNode instead directly broadcasting the operation.

1
2
3
struct ComputGraphStyle <: Broadcast.BroadcastStyle end
Base.BroadcastStyle(::Type{<:AbstractNode}) = ComputGraphStyle()
Broadcast.BroadcastStyle(s::ComputGraphStyle, x::Broadcast.BroadcastStyle) = s

However, this is not enough, in Julia broadcast is lazy-evaluated, which can fuse broadcast and provide better performance, we need to re-dispatch two interface: broadcasted and materialize

1
2
3
4
5
6
function Broadcast.broadcasted(::ComputGraphStyle, f, args...)
    mt = Trait.Broadcasted(f)
    register(mt, args...)
end

Broadcast.materialize(x::AbstractNode) = register(Broadcast.materialize, x)

And we let materialize directly return the gradient during backward evaluation:

1
2
3
4
5
function backward(node::CachedNode, ::typeof(Broadcast.materialize), grad)
    backward_type_assert(node, grad)
    @boundscheck backward_size_assert(node, grad)
    backward(node.node.args[1], grad) # materialize only has one arguments, we don't need the for loop
end

Now, if you try to broadcast with this AD, you would find that the assertion we defined in backward is quite annoying (because lazy evaluation, its output is not actually the real output, but a middle type), let’s mute them for broadcast:

1
2
3
4
5
6
7
function backward(node::CachedNode, ::Trait.Broadcasted, grad)
    grad_inputs = gradient(node, grad)
    for (each, each_grad) in zip(args(node), grad_inputs)
        backward(each, each_grad)
    end
    nothing
end

Add more operators for FREE!

There is a Julia package called DiffRules, it contains quite a lot differentiation rules defined as Julia Expr, so we can just use code generation to generate operators with it rather than define them ourselves:

The rules are in DiffRules.DEFINED_DIFFRULES, so we will just iterate through its key

1
2
3
for (mod, name, nargs) in keys(DiffRules.DEFINED_DIFFRULES)
  # code generation
end

the first argument mod is the module’s name, like for sin, it is actually in Base, so the mod is Base and
name is the function’s name, nargs means the number of arguments, in DiffRules, there are only single argument functions
and double arguments functions.

So the code generation will look like

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
for (mod, name, nargs) in keys(DiffRules.DEFINED_DIFFRULES)
    f_ex_head = Expr(:., mod, QuoteNode(name))

    if nargs == 1
        df_ex = DiffRules.diffrule(mod, name, :x)

        name === :abs && continue # exclude abs, it cannot be directly broadcasted

        @eval begin
            $(f_ex_head)(x::AbstractNode) = register($(f_ex_head), x)
            gradient(::typeof($(f_ex_head)), grad, output, x) = (grad * $df_ex, )
            gradient(mt::Trait.Broadcasted{typeof($f_ex_head)}, grad, output, x) = (@.(grad * $(df_ex)), )
        end
    elseif nargs == 2
        df_ex = DiffRules.diffrule(mod, name, :x, :y)

        @eval begin

            $(f_ex_head)(x1::AbstractNode, x2) = register($f_ex_head, x1, x2)
            $(f_ex_head)(x1, x2::AbstractNode) = register($f_ex_head, x1, x2)
            $(f_ex_head)(x1::AbstractNode, x2::AbstractNode) = register($f_ex_head, x1, x2)

            gradient(::typeof($f_ex_head), grad, output, x, y) =
                (grad * $(df_ex[1]), grad * $(df_ex[2]))
            gradient(::Trait.Broadcasted{typeof($f_ex_head)}, grad, output, x, y) =
                (@.(grad * ($(df_ex[1]))), @.(grad * $(df_ex[2])))
        end
    else
        @info "unknown operator $name"
    end
end

For how to use code generation in Julia, I would recommend the official documentation to get a better understanding of it: Code Generation. I escape abs here because the differentiation expression of abs generated by DiffRules can not be directly broadcasted by @. (this macro add a broadcast mark . to every function call), so I have to implement its gradient manually. But DiffRules will generate most of the math function’s gradient for you!

Polish

We roughly implemented the core functionality of an AD, but there’s still quite a lot to do to make it look and feel better.

I defined better printing later here: show.jl, the basic idea is to re-dispatch our nodes via several traits, so we can insert a type into another type tree, e.g as subtype of AbstractArray and then make use of existing printing methods.

Then, to implement unit tests, I copied the gradcheck function from PyTorch, which will calculate the jacobian of an operator with the AD package and compare it with the numerical jacobian.

Benchmark

Okay, it is done! With only about 200~300 lines Julia, what can we get? Actually, I thought it would be just a toy, but
it is actually amazing, when I tried to use it for my own work:

So I need to calculate something called matrix product state, well, I’m not going to talk about quantum physics, so in short, it is just some rank-3 tensors (3 dimensional array), and we will need to calculate something like the following expression:

1
tr(x1 * x2 * x3)

where x1, x2, x3 are just matrices.

So I implemented the gradient of tr and matrix multiplication:

1
2
3
4
5
6
7
8
9
10
11
12
Base.:(*)(lhs::AbstractNode, rhs) = register(Base.:(*), lhs, rhs)
Base.:(*)(lhs, rhs::AbstractNode) = register(Base.:(*), lhs, rhs)
Base.:(*)(lhs::AbstractNode, rhs::AbstractNode) = register(Base.:(*), lhs, rhs)

using LinearAlgebra

LinearAlgebra.tr(x::AbstractNode) = register(LinearAlgebra.tr, x)
gradient(::typeof(tr), grad, output, x) = (grad * Matrix(I, size(x)), )

function gradient(::typeof(*), grad, output, lhs::AbstractVecOrMat, rhs::AbstractVecOrMat)
    grad * transpose(rhs), transpose(lhs) * grad
end

Now let’s benchmark tr(x1 * x2) on the CPU with other packages, with the following function call

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
Zygote.@grad LinearAlgebra.tr(x) = LinearAlgebra.tr(x), Δ-> (Δ * Matrix(I, size(x)), )

function bench_tr_mul_yaad(x1, x2)
    z = tr(x1 * x2)
    YAAD.backward(z)
    x1.grad, x2.grad
end

function bench_tr_mul_autograd(x1, x2)
    z = AutoGrad.@diff tr(x1 * x2)
    AutoGrad.grad(z, x1), AutoGrad.grad(z, x2)
end

function bench_tr_mul_zygote(x1, x2)
    Zygote.gradient((x1, x2)->tr(x1 * x2), x1, x2)
end

function bench_tr_mul_flux(x1, x2)
    z = tr(x1 * x2)
    back!(z, 1)
    Tracker.grad(x1), Tracker.grad(x2)
end

and in PyTorch (our interface is quite similar to PyTorch, isn’t it?)

1
2
3
4
def bench_tr_mul_torch(x1, x2):
    z = torch.trace(torch.matmul(x1, x2))
    z.backward()
    return x1.grad, x2.grad

In Julia, we use BenchmarkTools to measure the time, and in Python we can use the magic command timeit in ipython.

The value is defined as follows

1
2
3
4
xv, yv = rand(30, 30), rand(30, 30)
yaad_x, yaad_y = YAAD.Variable(xv), YAAD.Variable(yv)
autograd_x, autograd_y = AutoGrad.Param(xv), AutoGrad.Param(yv)
flux_x, flux_y = Flux.param(xv), Flux.param(yv)

Before we benchmark other packages, I also wrote a baseline function, which calculates the gradient manually:

1
2
3
4
5
6
7
function bench_tr_mul_base(x1, x2)
    z1 = x1 * x2
    z2 = tr(z1)

    grad_z1 = Matrix{eltype(z1)}(I, size(z1))
    grad_z1 * transpose(x2), transpose(x1) * grad_z1
end

And then tests it with @benchmark, which will run this function multiple times

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
julia> @benchmark bench_tr_mul_autograd(autograd_x, autograd_y)
BenchmarkTools.Trial:
  memory estimate:  33.20 KiB
  allocs estimate:  82
  --------------
  minimum time:     50.218 μs (0.00% GC)
  median time:      62.364 μs (0.00% GC)
  mean time:        90.422 μs (9.86% GC)
  maximum time:     55.386 ms (99.86% GC)
  --------------
  samples:          10000
  evals/sample:     1

julia> @benchmark bench_tr_mul_yaad(yaad_x, yaad_y)
BenchmarkTools.Trial:
  memory estimate:  51.50 KiB
  allocs estimate:  16
  --------------
  minimum time:     10.387 μs (0.00% GC)
  median time:      13.429 μs (0.00% GC)
  mean time:        24.273 μs (45.13% GC)
  maximum time:     55.963 ms (99.96% GC)
  --------------
  samples:          10000
  evals/sample:     1

julia> @benchmark bench_tr_mul_zygote(xv, yv)
BenchmarkTools.Trial:
  memory estimate:  29.98 KiB
  allocs estimate:  10
  --------------
  minimum time:     42.527 μs (0.00% GC)
  median time:      46.640 μs (0.00% GC)
  mean time:        56.996 μs (15.31% GC)
  maximum time:     51.718 ms (99.90% GC)
  --------------
  samples:          10000
  evals/sample:     1

julia> @benchmark bench_tr_mul_base(xv, yv)
BenchmarkTools.Trial:
  memory estimate:  28.78 KiB
  allocs estimate:  5
  --------------
  minimum time:     6.413 μs (0.00% GC)
  median time:      8.201 μs (0.00% GC)
  mean time:        12.215 μs (31.57% GC)
  maximum time:     11.012 ms (99.87% GC)
  --------------
  samples:          10000
  evals/sample:     5

julia> @benchmark bench_tr_mul_flux(flux_x, flux_y)
BenchmarkTools.Trial:
  memory estimate:  30.25 KiB
  allocs estimate:  24
  --------------
  minimum time:     8.009 μs (0.00% GC)
  median time:      10.002 μs (0.00% GC)
  mean time:        14.412 μs (30.14% GC)
  maximum time:     16.286 ms (99.87% GC)
  --------------
  samples:          10000
  evals/sample:     3

and for PyTorch (version v0.4.1)

1
2
3
4
5
6
In [4]: x = torch.rand(30, 30, dtype=torch.float64, requires_grad=True)

In [5]: y = torch.rand(30, 30, dtype=torch.float64, requires_grad=True)

In [6]: %timeit bench_tr_mul_torch(x, y)
76.8 µs ± 1.68 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)

Our implementation is not bad, huh? Only about 4~5 μs slower than the baseline due to the dynamic construction of our computational graph in runtime and Flux is the fastest (it is implemented in similar approach), amazing! It is about 5x faster than other packages in either Julia or Python/C++.

So, as you see, writing an AD package can be super sweet in Julia with multiple dispatch. You can actually write your own AD with reasonable performance in Julia like a pro!

Acknowledgement

Thanks for Keno for benchmarking advice on Zygote, I was actually quite confused about the performance and submitted an issue here: Zygote.jl/issues/28

And thanks for the Luxor.jl package, I use this for plotting the animation in this blog post. You might want to check my ugly plotting script here: plot.jl

Finally, thanks for Travis Ashworth for helping me on polishing the blog post. This is actually my first time to blog in English, and I didn’t check this blog post carefully. And now I have two Travis (another Travis is the Travis-CI which builds my blog automatically.)

Welcome to my other publishing channels